梯度

梯度是一个向量，指向函数增长最快的方向。山体的陡峭程度

学习率

学习率决定了我们沿着梯度方向走多少步。学习率过大可能会导致我们越过最小值点，而学习率过小则可能导致收敛缓慢。

损失函数

用于评估训练出的模型的拟合程度，损失函数越大，意味着模型拟合的效果越差。

迭代

梯度下降法会计算损失函数的梯度，然后沿着梯度的反方向更新模型参数，这样可以在保持参数更新的方向与损失减少的方向一致的情况下，逐步减小损失函数的值。这个过程一直持续到梯度变得非常小，表明已经接近或达到了局部最小值。

梯度下降算法的用途

梯度下降法是机器学习中一种基础且重要的优化技术，尽管它不总是能找到全局最优解，但在实际应用中，通过合理的选择和调整，它可以非常有效地用于参数优化和模型训练。。

梯度下降算法的原理

梯度下降算法（Gradient Descent）是一种常用的优化算法，用于寻找函数的最小值或最大值。 它通过迭代的方式逐渐调整参数的取值，使得目标函数的值逐渐趋于最优解。

梯度下降算法公式

theta = theta – alpha * (partial J (theta) / partial theta)，其中theta是待求的参数，alpha是学习率，J (theta)是目标函数

另一种形式的公式为：theta_ {t+1} = theta_t – eta nabla f_i (theta_t)，其中theta表示模型参数，eta是学习率，f_i是损失函数

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(42)
x = np.random.rand(50, 1)
y = 4 * x + 0.5 * np.random.randn(50, 1)

w = 0
b = 0

ate = 0.1
iterations = 1000

def descend(x, y, w, b, ate):
    loss = 0
    mpd = 0
    bpd = 0
    N = x.shape[0]

    for i, j  in zip(x, y):
        loss += (w * i + b - j ) ** 2
        bpd += 2 * (w * i + b - j)
        mpd += 2 * i * (w * i + b - j)

    loss = loss / N
    mpd = mpd / N
    bpd = bpd / N

    w = w - mpd * ate
    b = b - bpd * ate

    return loss, w, b

for epoch in range(iterations):
    loss, w, b = descend(x, y, w, b, ate)

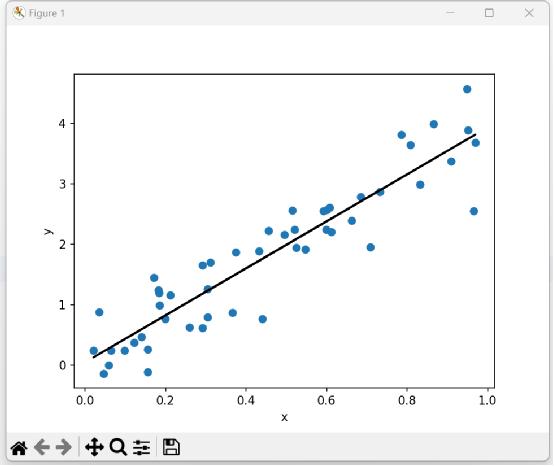
plt.scatter(x, y)
plt.plot(x, w * x + b, color='k')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

学习报告

在进行任务二之前，首先需要了解熟练python语言的应用，其次要对数据可视化有相当程度的了解，最后是知道什么是梯度下降算法。这个过程需要消耗大量的时间和大量的精力，由于学校没有开设python语言课程，所以自学需要耗费的精力是更多的，也需要一定的理解力。在了解梯度下降算法的同时也知道了梯度下降算法的由来及梯度下降算法干什么用。

在我的理解中，梯度下降算法就是选择一个最短的路径，比如一座高山，通过比较每一条路，每次都选择一条最陡峭的路往下走，当下降到指定地方，又选择一条最陡峭的路，如此循环往复，一直到最低点为止。实际上，梯度下降有多种方法，我选择的方法是MBGD方法，每次更新使用批量样本的梯度通常在计算效率和收敛速度之间取得平衡。计算所有样本点与直线的偏离程度，通过误差大小来调整直线的斜率，

再计算误差平方和的平均值。

在学习梯度下降时需要查阅大量资料和视频，有些资料难以理解，有些资料残缺不全，有些视频讲解较好，使我深刻了解了梯度下降算法。